离散数学习题解答.doc 32页

'离散数学习题答案习题一1.判断下列句子是否为命题？若是命题说明是真命题还是假命题。（1）3是正数吗？（2）x＋1=0。（3）请穿上外衣。（4）2＋1＝0。（5）任一个实数的平方都是正实数。（6）不存在最大素数。（7）明天我去看电影。（8）9＋5≤12。（9）实践出真知。（10）如果我掌握了英语、法语，那么学习其他欧洲语言就容易多了。解：（1）、（2）、（3）不是命题。（4）、（8）是假命题。（5）、（6）、（9）、（10）是真命题。（7）是命题，只是现在无法确定真值。2.设P表示命题“天下雪”，Q表示命题“我将去书店”，R表示命题“我有时间”，以符号形式写出下列命题。（1）如果天不下雪并且我有时间，那么我将去书店。（2）我将去书店，仅当我有时间。（3）天不下雪。（4）天下雪，我将不去书店。解：（1）（┐P∧R）→Q。（2）Q→R。（3）┐P。（4）P→┐Q。3.将下列命题符号化。（1）王皓球打得好，歌也唱得好。（2）我一边看书，一边听音乐。（3）老张和老李都是球迷。（4）只要努力学习，成绩会好的。（5）只有休息好，才能工作好。（6）如果a和b是偶数，那么a+b也是偶数。（7）我们不能既游泳又跑步。（8）我反悔，仅当太阳从西边出来。（9）如果f(x)在点x0处可导，则f(x)在点x0处可微。反之亦然。（10）如果张老师和李老师都不讲这门课，那么王老师就讲这门课。（11）四边形ABCD是平行四边形，当且仅当ABCD的对边平行。（12）或者你没有给我写信，或者信在途中丢失了。解： （1）P：王皓球打得好，Q：王皓歌唱得好。原命题可符号化：P∧Q。（2）P：我看书，Q：我听音乐。原命题可符号化：P∧Q。（3）P：老张是球迷，Q：老李是球迷。原命题可符号化：P∧Q。（4）P：努力学习，Q：成绩会好。原命题可符号化：P→Q。（5）P：休息好，Q：工作好。原命题可符号化：Q→P。（6）P：a是偶数，Q：b是偶数，R：a+b是偶数。原命题可符号化：（P∧Q）→R。（7）P：我们游泳，Q：我们跑步。原命题可符号化：┐（P∧Q）。（8）P：我反悔，Q：太阳从西边出来。原命题可符号化：P→Q。（9）P：f(x)在点x0处可导，Q：f(x)在点x0处可微。原命题可符号化：P→←Q。（10）P：张老师讲这门课，Q：李老师讲这门课，R：王老师讲这门课。原命题可符号化：（┐P∧┐Q）→R。（11）P：四边形ABCD是平行四边形，Q：四边形ABCD的对边平行。原命题可符号化：P→←Q。（12）P：你给我写信，Q：信在途中丢失了。原命题可符号化：┐P←∣→（P∧Q）。4.判断下列公式哪些是合式公式，哪些不是合式公式。（1）(Q→R∧S)（2）(P→←(R→S))（3）((┐P→Q)→(Q→P)))（4）(RS→F)（5）((P→(Q→R))→((P→Q)→(P→R)))解：（1）、（2）、（5）是合式公式，（3）、（4）不是合式公式。5.否定下列命题：（1）桂林处处山清水秀。（2）每一个自然数都是偶数。解：（1）桂林并非处处山清水秀。（2）并不是每一个自然数都是偶数。或：有些自然数不是偶数。6.给出下述每一个命题的逆命题、否命题和逆否命题。（1）如果天下雨，我将不去。（2）仅当你去我才不去。（3）如果Δ=b2−4ac<0，则方程ax2+bx+c=0无实数解。（4）如果我不获得奖学金，我就不能完成学业。解：（1）逆命题：如果我不去，那么天下雨。否命题：如果天不下雨，我就去。逆否命题：如果我去，那么天不下雨。（2）逆命题：如果你去，我将不去。否命题：如果我去，你将不去。逆否命题：如果你不去，我就去。（3）逆命题：如果方程ax2+bx+c=0无实数解，则Δ=b2−4ac<0。否命题：如果Δ=b2−4ac≥0，则方程ax2+bx+c=0有实数解。逆否命题：如果方程ax2+bx+c=0有实数解，则Δ=b2−4ac≥0。（4）逆命题：如果我不能完成学业，那么我没有获得奖学金。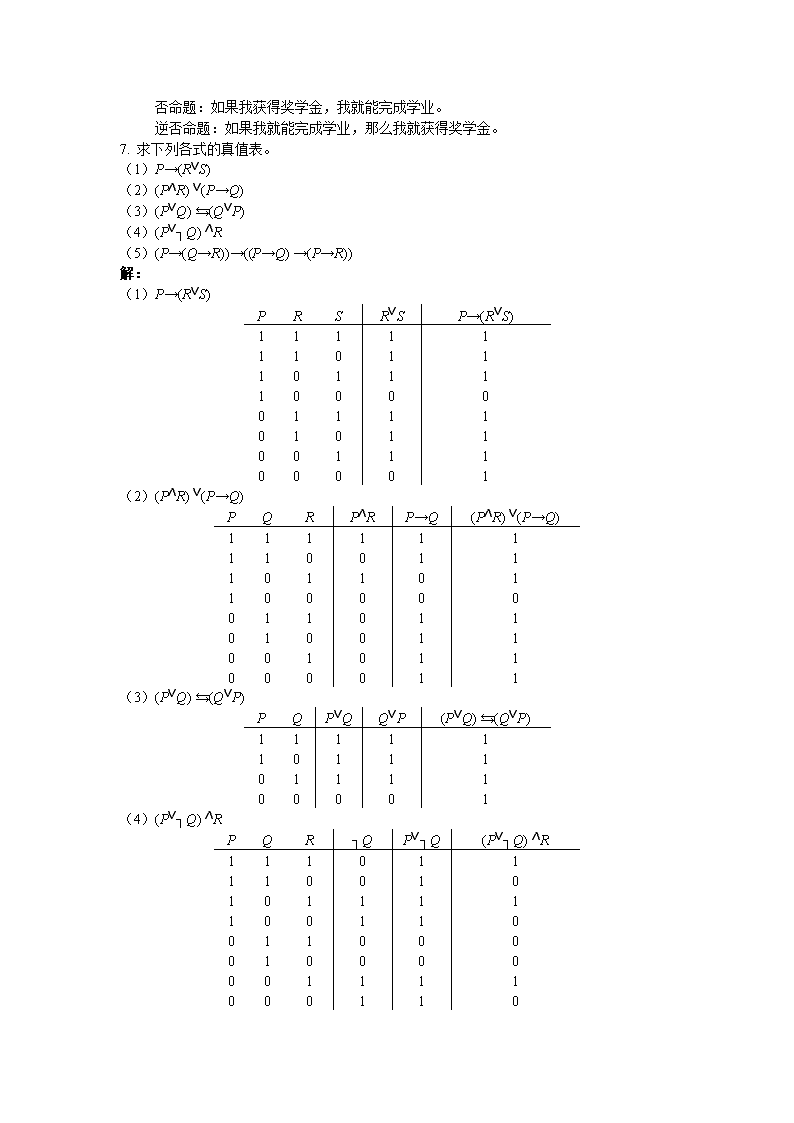 否命题：如果我获得奖学金，我就能完成学业。逆否命题：如果我就能完成学业，那么我就获得奖学金。7.求下列各式的真值表。（1）P→(R∨S)（2）(P∧R)∨(P→Q)（3）(P∨Q)→←(Q∨P)（4）(P∨┐Q)∧R（5）(P→(Q→R))→((P→Q)→(P→R))解：（1）P→(R∨S)PRSR∨SP→(R∨S)1111111011101111000001111010110011100001（2）(P∧R)∨(P→Q)PQRP∧RP→Q(P∧R)∨(P→Q)111111110011101101100000011011010011001011000011（3）(P∨Q)→←(Q∨P)PQP∨QQ∨P(P∨Q)→←(Q∨P)11111101110111100001（4）(P∨┐Q)∧RPQR┐QP∨┐Q(P∨┐Q)∧R111011110010101111100110011000010000001111000110 （5）(P→(Q→R))→((P→Q)→(P→R))PQRQ→RP→(Q→R)P→QP→R(P→Q)→(P→R)原公式1111111111100010011011101111001100110111111110100111110011111110001111118.用真值表判断下列公式的类型：(1)P∨┐Q→Q(2)((P→Q)∨(R→S))→((P∨R)→(Q∨S))解：(1)P∨┐Q→QPQ┐QP∨┐QP∨┐Q→Q11011101100100100110（1）为可满足式。(2)((P→Q)∨(R→S))→((P∨R)→(Q∨S))PQRSP→QR→S(P→Q)∨(R→S)P∨RQ∨S(P∨R)→(Q∨S)原公式11111111111111010111111101111111111001111111101101111111010000100110010111111100001110000111111111101101001111010111101110100111011100111111111001010110000001111011100001110011（2）为可满足式。9.证明下列等价式。（1）P→(Q→P)Û┐P→(P→┐Q)（2）┐(P→←Q)Û(P∨Q)∧┐(P∧Q)（3）┐(P→Q)ÛP∧┐Q（4）┐(P→←Q)Û(P∧┐Q)∨(┐P∧Q) （5）P→(Q∨R)Û(P∧┐Q)→R（6）(P→R)∧(Q→R)Û(P∨Q)→R（7）((P∧Q)→R)∧(Q→(S∨R))Û(Q∧(S→P))→R证明：（1）P→(Q→P)Û┐P∨(┐Q∨P)ÛP∨(┐P∨┐Q)Û┐P→(P→┐Q)（2）┐(P→←Q)Û┐((P∧Q)∨(┐P∧┐Q))Û┐(P∧Q)∧┐(┐P∧┐Q))Û(P∨Q)∧┐(P∧Q)（3）┐(P→Q)Û┐(┐P∨Q)ÛP∧┐Q（4）┐(P→←Q)Û┐((P→Q)∧(Q→P))Û┐(┐P∨Q)∨┐(┐Q∨P)Û(P∧┐Q)∨(┐P∧Q)（5）P→(Q∨R)Û┐P∨(Q∨R)Û┐(P∧┐Q)∨RÛ(P∧┐Q)→R（6）(P→R)∧(Q→R)Û(┐P∨R)∧(┐Q∨R)Û(┐P∧┐Q)∨RÛ┐(P∨Q)∨RÛ(P∨Q)→R（7）((P∧Q)→R)∧(Q→(S∨R))Û(┐(P∧Q)∨R)∧(┐Q∨(S∨R))Û┐Q∨(┐P∧S)∨RÛ┐(Q∧(┐S∨P))∨RÛ┐(Q∧(S→P))∨RÛ(Q∧(S→P))→R10.使用恒等式证明下列各式，并写出它们对偶的公式。（1）(┐(┐P∨┐Q)∨┐(┐P∨Q))⇔P（2）(P∨┐Q)∧(P∨Q)∧(┐P∨┐Q)⇔┐(┐P∨Q)（3）Q∨┐((┐P∨Q)∧P)⇔T证明：（1）(┐(┐P∨┐Q)∨┐(┐P∨Q))⇔(P∧Q)∨(P∧┐Q)⇔P∧(Q∨┐Q)⇔P∧T⇔P（2）(P∨┐Q)∧(P∨Q)∧(┐P∨┐Q)⇔P∨(┐Q∧Q)∧(┐P∨┐Q)⇔P∨F∧(┐P∨┐Q)⇔P∧(┐P∨┐Q)⇔(P∧┐P)∨(P∧┐Q)⇔F∨(P∧┐Q)⇔(P∧┐Q)⇔┐(┐P∨Q)（3）Q∨┐((┐P∨Q)∧P)⇔Q∨(┐(┐P∨Q)∨┐P)⇔Q∨(P∧┐Q)∨┐P⇔(Q∨┐P∨P)∧(Q∨┐P∨┐Q)⇔T∨T⇔T11.试证明{∨}，{→}不是全功能联结词集合。证明：若{∨}是最小联结词组，则┐P⇔(P∨...)对所有命题变元指派T，则等价式左边为F，右边为T，等价式矛盾。若{→}是最小联结词组，则┐P⇔P→(P→(P→...)...)对所有命题变元指派T，则等价式左边为F，右边为T，等价式矛盾。12.证明下列蕴涵式：（1）P∧Q⇒(P→Q)（2）P⇒(Q→P)（3）(P→(Q→R))⇒(P→Q)→(P→R)证明：（1）P∧Q→(P→Q)⇔┐(P∧Q)∨(P→Q)⇔(┐P∨┐Q)∨(┐P∨Q)⇔┐P∨(┐Q∨Q)⇔T因为P∧Q→(P→Q)为永真式，所以P∧Q⇒(P→Q)。（2）P→(Q→P)⇔┐P∨(┐Q∨P)⇔┐Q∨(┐P∨P)⇔T因为P→(Q→P)为永真式，所以P⇒(Q→P)。（3）(P→(Q→R))→((P→Q)→(P→R))⇔┐(┐P∨(┐Q∨R))∨(┐(┐P∨Q)∨(┐P∨R))⇔(P∧(Q∧┐R))∨((P∧┐Q)∨(┐P∨R))⇔(P∧Q∧┐R)∨((P∨┐P∨R)∧(┐Q∨┐P∨R))⇔(P∧Q∧┐R)∨(┐P∨┐Q∨R)⇔((P∨(┐P∨┐Q∨R))∧(Q∨(┐P∨┐Q∨R))∧(┐R∨(┐P∨┐Q∨R))⇔T因为(P→(Q→R))→((P→Q)→(P→R))为永真式，所以(P→(Q→R))⇒(P→Q)→(P→R)。 13.对下列各公式，试仅用↑或↓表示。（1）┐P（2）P∧Q（3）P∨Q（4）P→Q解：（1）┐P⇔┐(P∧P)⇔P↑P（2）P∧Q⇔(P↑Q)↑(P↑Q)（3）P∨Q⇔┐(┐P∧┐Q)⇔(┐P↑┐Q)⇔(P↑P)↑(Q↑Q)（4）P→Q⇔┐P∨Q⇔(P↑P)∨Q⇔((P↑P)↑(P↑P))↑(Q↑Q)14.将下列公式化成与之等值且仅含{┐，→}中联结词的公式。（1）(P→┐Q)∧R（2）P→←(Q∧R)∨P解：（1）(P→┐Q)∧R⇔(┐P∨┐Q)∧R⇔(┐P∧R)∨(┐Q∧R)⇔┐(P∨┐R)∨┐(Q∨┐R)⇔┐(R→P)∨┐(R→Q)⇔(R→P)→┐(R→Q)（2）P→←(Q∧R)∨P⇔(P→((Q∧R)∨P))∧(((Q∧R)∨P)→P)⇔(┐P∨((Q∧R)∨P))∧(┐((Q∧R)∨P)∨P)⇔T∧(((┐Q∨┐R)∧┐P)∨P)⇔((┐Q∨┐R)∨P)⇔P∨(┐Q∨┐R)⇔P∨(Q→┐R)⇔┐P→(Q→┐R)15.如果A(P，Q，R)由R↑(Q∧┐(R↓P))给出，求它的对偶A*(P，Q，R)，并求出与A及A*等价且仅包含联接词“∧”，“∨”及“┐”的公式。解：A*(P，Q，R)：R↓(Q∨┐(R↑P))R↑(Q∧┐(R↓P))⇔┐(R∧(Q∧(R∨P)))⇔┐R∨┐Q∨(┐R∧┐P)R↓(Q∨┐(R↑P))⇔┐R∧┐Q∧(┐R∨┐P)16.把P↑Q表示为只含有“↓”的等价公式。解：P↑QÛ┐(P∧Q)Û┐((P↓P)↓(Q↓Q))Û((P↓P)↓(Q↓Q))↓((P↓P)↓(Q↓Q))17.证明：（1）┐(P↑Q)Û┐P↓┐Q（2）┐(P↓Q)Û┐P↑┐Q证明：（1）┐(P↑Q)Û┐(┐(P∧Q))Û(P∧Q)Û┐(┐P∨┐Q)Û┐P↓┐Q（2）┐(P↓Q)Û┐(┐(P∨Q))Û(P∨Q)Û┐(┐P∧┐Q)Û┐P↑┐Q18.求公式P∧(P→Q)的析取范式和合取范式。解：P∧(P→Q)ÛP∧(┐P∨Q)合取范式Û(P∧┐P)∨(P∧Q)析取范式19.求下列公式的主析取范式和主合取范式。（1）(┐P→Q)→(┐Q∨P)（2）(P→(P∨Q))∨R（3）(P→Q∧R)∧((┐P→(┐Q∧┐R))解：（1）真值表法PQ┐P→Q┐Q∨P(┐P→Q)→(┐Q∨P)11111 101110110000011主析取范式为：(P∧Q)∨(P∧┐Q)∨(┐P∧┐Q)主合取范式为：P∨┐Q公式化归法(┐P→Q)→(┐Q∨P)Û┐(P∨Q)∨(┐Q∨P)Û(┐P∧┐Q)∨(┐Q∨P)Û(┐P∨┐Q∨P)∧(┐Q∨┐Q∨P)ÛP∨┐Q主合取范式Û(P∧Q)∨(P∧┐Q)∨(┐P∧┐Q)主析取范式（2）真值表法(P→(P∨Q))∨RPQRP∨QP→(P∨Q)(P→(P∨Q))∨R111111110111101111100111011111010111001011000011原式为永真式，其主析取范式为所有小项的析取，即：m000∨m001∨m010∨m011∨m100∨m101∨m110∨m111不能表示为主合取范式。公式化归法(P→(P∨Q))∨RÛ(┐P∨(P∨Q))∨RÛT∨RÛT（3）真值表法(P→Q∧R)∧((┐P→(┐Q∧┐R))PQRQ∧RP→Q∧R┐Q∧┐R┐P→(┐Q∧┐R)原公式1111101111000010101000101000011001111000010010000010100000001111主析取范式为：(P∧Q∧R)∨(┐P∧┐Q∧┐R)Ûm111∨m000Ûm7∨m0主合取范式为：M1∧M2∧M3∧M4∧M5∧M6ÛM001∧M010∧M011∧M100∧M101∧M110Û(P∨Q∨┐R)∧(P∨┐Q∨R)∧(P∨┐Q∨┐R)∧(┐P∨Q∨R)∧(┐P∨Q∨┐R)∧(┐P∨┐Q∨R)20.求下列公式的主析取范式和主合取范式，并指出该公式的类型。（1）(┐P∨┐Q)→(P→←┐Q)（2）Q∧(P∨┐Q)（3）P∨(┐P→(Q∨(┐Q→R)))（4）(P→(Q∧R))∧(┐P→(┐Q∧┐R))（5）P→(P∧(Q→P))（6）(Q→P)∧(┐P∧Q)解： （1）PQ┐P∨┐QP→←┐Q(┐P∨┐Q)→(P→←┐Q)11001101110111100100主析取范式为：(P∧Q)∨(P∧┐Q)∨(┐P∧Q)主合取范式为：P∨Q公式为可满足式。（2）PQP∨┐QQ∧(P∨┐Q)1111101001000010主析取范式为：P∧Q主合取范式为：(┐P∨Q)∧(P∨┐Q)∧(P∨Q)公式为可满足式。（3）P∨(┐P→(Q∨(┐Q→R)))ÛP∨(P∨(Q∨(Q∨R)))ÛP∨Q∨R主合取范式ÛM000ÛM0Ûm1∨m2∨m3∨m4∨m5∨m6∨m7主析取范式公式为可满足式。（4）(P→(Q∧R))∧(┐P→(┐Q∧┐R))Û(┐P∨(Q∧R))∧(P∨(┐Q∧┐R))Û(┐P∨Q)∧(┐P∨R)∧(P∨┐Q)∧(P∨┐R)Û(┐P∨Q∨R)∧(┐P∨Q∨┐R)∧(┐P∨┐Q∨┐R)∧(P∨┐Q∨R)∧(P∨┐Q∨┐R)∧(P∨Q∨┐R)ÛM100∧M101∧M111∧M010∧M011∧M001ÛM4∧M5∧M7∧M2∧M3∧M1主合取范式Ûm0∨m6Ûm000∨m110主析取范式公式为可满足式。（5）P→(P∧(Q→P))Û┐P∨(P∧(┐Q∨P))Û(┐P∨P)∧(┐P∨(┐Q∨P))ÛT主析取范式为：m0∨m1∨m2∨m3公式为永真式。（6）(Q→P)∧(┐P∧Q)Û(┐Q∨P)∧(┐P∧Q)Û(┐Q∧┐P∧Q)∨(P∧┐P∧Q)ÛF主合取范式为：M0∧M1∧M2∧M3公式为永假式。21.用将合式公式化为范式的方法证明下列各题中两式是等价的。（1）(P→Q)∧(P→R)，P→(Q∧R)（2）(P→Q)→(P∧Q)，(┐P→Q)∧(Q→P)（3）P∧Q∧(┐P∨┐Q)，┐P∧┐Q∧(P∨Q)（4）P∨(P→(P∧Q))，┐P∨┐Q∨(P∧Q)证明：（1）(P→Q)∧(P→R)Û(┐P∨Q)∧(┐P∨R)P→(Q∧R)Û┐P∨(Q∧R)Û(┐P∨Q)∧(┐P∨R)（2）(P→Q)→(P∧Q)Û┐(┐P∨Q)∨(P∧Q)Û(P∧┐Q)∨(P∧Q)ÛP∧(┐Q∨Q)ÛP(┐P→Q)∧(Q→P)Û(P∨Q)∧(┐Q∨P)ÛP∨(Q∧┐Q)ÛP （3）P∧Q∧(┐P∨┐Q)Û(P∧Q∧┐P)∨(P∧Q∧┐Q)ÛF┐P∧┐Q∧(P∨Q)Û(┐P∧┐Q∧P)∨(┐P∧┐Q∧Q)ÛF（4）P∨(P→(P∧Q))ÛP∨(┐P∨(P∧Q))ÛT∨(P∧Q)ÛT┐P∨┐Q∨(P∧Q)Û(┐P∨┐Q∨P)∧(┐P∨┐Q∨Q)ÛT22.用推理规则证明以下各式。（1）┐(P∧┐Q)，┐Q∨R，┐R⇒┐P（2）A→(B∨C)，(D∨E)→A，D∨E⇒B∨C（3）B∧C，(B→←C)→(D∨E)⇒D∨E（4）P→Q，(┐Q∨R)∧┐R，┐(┐P∧S)⇒┐S证明：（1）┐(P∧┐Q)，┐Q∨R，┐R⇒┐P证明：(1)┐RP(2)┐Q∨RP(3)┐QT(1)(2)I(4)┐(P∧┐Q)P(5)┐P∨QT(4)E(6)┐PT(3)(5)I（2）A→(B∨C)，(D∨E)→A，D∨E⇒B∨C证明：(1)D∨EP(2)(D∨E)→AP(3)AT(1)(2)I(4)A→(B∨C)P(5)B∨CT(3)(4)I（3）B∧C，(B→←C)→(D∨E)⇒D∨E证明：(1)B∧CP(2)B→←CT(1)I(3)(B→←C)→(D∨E)P(4)D∨ET(2)(3)I（4）P→Q，(┐Q∨R)∧┐R，┐(┐P∧S)⇒┐S证明：(1)(┐Q∨R)∧┐RP(2)┐Q∨RT(1)I(3)┐RT(1)I(4)┐QT(2)(3)I(5)┐(┐P∧S)P(6)S→PT(5)E(7)P→QP(8)S→QT(6)(7)I(9)┐Q→┐ST(8)E(10)┐ST(4)(8)I23.仅用规则P和T，推证以下公式。 （1）┐A∨B，C→┐B⇒A→┐C（2）A→(B→C)，(C∧D)→E，┐F→(D∧┐E)⇒A→(B→F)（3）A∨B→C∧D，D∨E→F，⇒A→F（4）A→(B∧C)，┐B∨D，(E→┐F)→┐D，B→(A∧┐E)⇒B→E（5）(A→B)∧(C→D)，(B→E)∧(D→F)，┐(E∧F)，A→C⇒┐A证明：（1）┐A∨B，C→┐B⇒A→┐C证明：(1)┐A∨BP(2)A→BT(1)E(3)C→┐BP(4)B→┐CT(3)E(5)A→┐CT(2)(4)I（2）A→(B→C)，(C∧D)→E，┐F→(D∧┐E)⇒A→(B→F)证明：(1)A→(B→C)P(2)┐A∨┐B∨CT(1)E(3)(A∧B)→CT(2)E(4)(C∧D)→EP(5)C→┐(D∧┐E)T(4)E(6)(D∧┐E)→┐CT(5)E(7)┐F→(D∧┐E)P(8)┐F→┐CT(6)(7)I(9)C→FT(8)E(10)(A∧B)→FT(3)(9)I(11)┐A∨┐B∨FT(10)E(12)A→(B→F)T(11)E（3）A∨B→C∧D，D∨E→F⇒A→F证明：(1)A∨B→C∧DP(2)A∨B→DT(1)I(3)D∨E→FP(4)D→FT(3)I(5)A∨B→FT(2)(4)I(6)A→FT(5)I（4）A→(B∧C)，┐B∨D，(E→┐F)→┐D，B→(A∧┐E)⇒B→E证明：(1)┐B∨DP(2)B→DT(1)E(3)(E→┐F)→┐DP(4)D→┐(E→┐F)T(3)E(5)D→(E∧F)T(4)E(6)B→(E∧F)T(2)(5)I(7)B→ET(6)I （5）(A→B)∧(C→D)，(B→E)∧(D→F)，┐(E∧F)，A→C⇒┐A证明：(1)(A→B)∧(C→D)P(2)A→BT(1)I(3)C→DT(1)I(4)(B→E)∧(D→F)P(5)B→ET(4)I(6)D→FT(4)I(7)A→ET(2)(5)I(8)C→FT(3)(6)I(9)A→CP(10)A→FT(8)(9)I(11)A→(E∧F)T(7)(10)I(12)┐(E∧F)→┐AT(11)E(13)┐(E∧F)P(14)┐AT(12)(13)I24.用CP规则推证上题中的（1）、（2）、（3）和（4）式。证明：（1）┐A∨B，C→┐B⇒A→┐C证明：(1)AP（附加前提）(2)┐A∨BP(3)BT(1)(2)I(4)C→┐BP(5)┐CT(3)(4)I(6)A→┐CT(1)(5)CP（2）A→(B→C)，(C∧D)→E，┐F→(D∧┐E)⇒A→(B→F)证明：(1)AP（附加前提）(2)A→(B→C)P(3)B→CT(1)(2)I(4)(C∧D)→EP(5)C→┐(D∧┐E)T(4)E(6)B→┐(D∧┐E)T(3)(5)I(7)┐F→(D∧┐E)P(8)┐(D∧┐E)→FT(7)E(9)B→FT(6)(8)I(10)A→(B→F)CP(1)(9)（3）A∨B→C∧D，D∨E→F⇒A→F证明：(1)AP（附加前提）(2)A∨BT(1)I(3)A∨B→C∧DP(4)C∧DT(2)(3)I (5)DT(4)I(6)D∨ET(5)I(7)D∨E→FP(8)FT(6)(7)I(9)A→FCP(5)(8)（4）A→(B∧C)，┐B∨D，(E→┐F)→┐D，B→(A∧┐E)⇒B→E证明：(1)BP（附加前提）(2)┐B∨DP(3)DT(1)(2)I(4)(E→┐F)→┐DP(5)D→┐(E→┐F)T(4)E(6)┐(E→┐F)T(3)(5)I(7)E∧FT(6)E(8)ET(7)I(9)B→ECP(1)(8)25.证明下列各式。（1）R→┐Q，R∨S，S→┐Q，P→Q⇒┐P（2）S→┐Q，R∨S，┐R，┐P→←Q⇒P（3）┐(P→Q)→┐(R∨S)，(Q→P)∨┐R，R⇒P→←Q证明：（1）R→┐Q，R∨S，S→┐Q，P→Q⇒┐P证明：(1)PP(附加前提)(2)P→QP(3)QT(1)(2)I(4)R→┐QP(5)S→┐QP(6)Q→┐RT(4)E(7)Q→┐ST(5)E(8)┐RT(3)(6)I(9)┐ST(3)(7)I(10)┐R∧┐ST(8)(9)I(11)┐(R∨S)T(10)E(12)R∨SP(13)┐(R∨S)∧(R∨S)(矛盾)T(12)(13)I（2）S→┐Q，R∨S，┐R，┐P→←Q⇒P证明：(1)┐RP(2)R∨SP(3)ST(1)(2)I(4)S→┐QP(5)┐QT(3)(4)I(6)┐P→←QP (7)(┐P→Q)∧(Q→┐P)T(6)E(8)┐P→QT(7)I(9)┐Q→PT(8)E(10)PT(5)(9)I（3）┐(P→Q)→┐(R∨S)，(Q→P)∨┐R，R⇒P→←Q证明：(1)RP(2)(Q→P)∨┐RP(3)Q→PT(1)(2)I(4)┐(P→Q)→┐(R∨S)P(5)(R∨S)→(P→Q)T(4)E(6)P→QT(1)(5)I(7)(P→Q)∧(Q→P)T(3)(6)I(8)P→←QT(7)E26.甲、乙、丙和丁四人参加考试，有人问他们，谁的成绩最好？甲说“不是我”，乙说“是丁”，丙说“是乙”，丁说“不是我”。四人的回答只有一人符合实际。问成绩最好的是哪些？若只有一人成绩最好，是谁？解：设A：甲的成绩最好。B：乙的成绩最好。C：丙的成绩最好。D：丁的成绩最好。因为四人的回答只有一人符合实际，所以若甲的回答符合实际，有：(┐A∧┐D∧┐B∧D)若乙的回答符合实际，有：(A∧D∧┐B∧D)若丙的回答符合实际，有：(A∧┐D∧B∧D)若丁的回答符合实际，有：(A∧┐D∧┐B∧┐D)所以：(┐A∧┐D∧┐B∧D)∨(A∧D∧┐B∧D)∨(A∧┐D∧B∧D)∨(A∧┐D∧┐B∧┐D)ÛT即(A∧D∧┐B)∨(A∧┐D∧┐B)ÛT但(A∧D∧┐B)∨(A∧┐D∧┐B)Û(A∧D∧┐B∧C)∨(A∧D∧┐B∧┐C)∨(A∧┐D∧┐B∧C)∨(A∧┐D∧┐B∧┐C)(A∧D∧┐B∧C)表示甲、丙和丁三人并列成绩最好。(A∧D∧┐B∧┐C)表示甲、丁两人并列成绩最好。(A∧┐D∧┐B∧C)表示甲、丙两人并列成绩最好。(A∧┐D∧┐B∧┐C)表示甲成绩最好。若只有一人成绩最好，是甲。27.三人估计比赛结果，甲说“A第一，B第二”。乙说“C第二，D第四”。丙说“A第二，D第四”。结果三人估计得都不全对，但都对了一个，问A、B、C、D的名次。解：设A：A第一。B：B第二。C：C第二。D：D第四。E：A第二。根据题意有：(A←∣→B)∧(C←∣→D)∧(E←∣→D)成立。将其化为析取范式的形式：(A←∣→B)∧(C←∣→D)∧(E←∣→D)Û((A∧┐B)∨(┐A∧B))∧((C∧┐D)∨(┐C∧D))∧((E∧┐D)∨(┐E∧D))Û((A∧┐B∧C∧┐D)∨(A∧┐B∧┐C∧D)∨(┐A∧B∧C∧┐D)∨(┐A∧B∧┐C∧D))∧((E∧┐D)∨(┐E∧D))其中(A∧┐B∧┐C∧D)和(┐A∧B∧C∧┐D)不复合题意，可以从上式中删去，原式化为：((A∧┐B∧C∧┐D)∨(┐A∧B∧┐C∧D))∧((E∧┐D)∨(┐E∧D))Û(A∧┐B∧C∧┐D∧E∧┐D)∨(┐A∧B∧┐C∧D∧E∧┐D)∨(A∧┐B∧C∧┐D∧┐E ∧D)∨(┐A∧B∧┐C∧D∧┐E∧D)Û(A∧┐B∧C∧┐D∧E)∨(┐A∧B∧┐C∧D∧┐E)(A∧┐B∧C∧┐D∧E)中C和E)同时成立矛盾，故只能是(┐A∧B∧┐C∧D∧┐E)成立，即B第二，D第四，A第三，C第一。28.A，B，C，D四个人中要派两个人出差，按下述三个条件有几种派法？如何派？（1）若A去则C和D要去一人；（2）B和C不能都去；（3）C去则D要留下。解：设A：A去。B：B去。C：C去。D：D去。则（1）可表示为：A→(C←∣→D)；（2）可表示为：┐(B∧C)；（3）可表示为：C→┐D。(1)(2)(3)同时成立，即A→(C←∣→D)∧┐(B∧C)∧(C→┐D)成立。将其化为析取范式的形式：A→(C←∣→D)∧┐(B∧C)∧(C→┐D)Û(┐A∨(┐C∧D)∨(C∧┐D))∧(┐B∨┐C)∧(┐C∨┐D)Û(┐A∨(┐C∧D)∨(C∧┐D))∧((┐B∧┐C)∨(┐B∧┐D)∨┐C∨(┐C∧┐D))Û(┐A∧┐B∧┐C)∨(┐A∧┐B∧┐D)∨(┐A∧┐C)∨(┐A∧┐C∧┐D)∨(┐C∧D∧┐B∧┐C)∨(┐C∧D∧┐B∧┐D)∨(┐C∧D∧┐C)∨(┐C∧D∧┐C∧┐D)∨(C∧┐D∧┐B∧┐C)∨(C∧┐D∧┐B∧┐D)∨(C∧┐D∧┐C)∨(C∧┐D∧┐C∧┐D)Û(┐A∧┐B∧┐C)∨(┐A∧┐B∧┐D)∨(┐A∧┐C)∨(┐A∧┐C∧┐D)∨(┐B∧┐C∧D)∨(┐C∧D)∨(┐B∧C∧┐D)上式划线的部分不符合题意，因此复合题意的有：(┐A∧┐C)∨(┐B∧┐C∧D)∨(┐C∧D)∨(┐B∧C∧┐D)，(┐A∧┐C)表示B和D去，(┐B∧┐C∧D)表示A和D去，(┐C∧D)表示A和D去或B和D去，(┐B∧C∧┐D)表示A和C去。故总共有三种派法：B和D去，A和D去或A和C去。29.在一个盗窃案件中，已知下列事实：（1）甲或乙是窃贼。（2）甲是窃贼，作案时间不会发生在夜间12点以前。（3）若乙的证词正确，则夜间12点时被盗物品所在房间灯光未灭。（4）若乙的证词不正确，则作案时间发生在夜间12点以前。（5）夜间12点被盗房间的灯光灭了。判断谁是盗贼，用构造证明法写出结论的判断过程。证明：设A：甲是窃贼。B：乙是窃贼。C：作案时间发生在夜间12点以前。D：乙的证词正确。E：夜间12点被盗房间的灯光灭了。则（1）可以表示为：A∨B。（2）可以表示为：A→┐C。（3）可以表示为：D→┐E。（4）可以表示为：┐D→C。（5）可以表示为：E。以下是推理过程：(1)EP(2)D→┐EP(3)┐DT(1)(2)I(4)┐D→CP(5)CT(3)(4)I(6)A→┐CP(7)┐AT(5)(6)I(8)A∨BP(9)BT(7)(8)I 所以B成立，即乙是窃贼。30.构造下面推理的证明：（1）如果今天是星期六，我们就要到独秀峰或象鼻山去玩，如果独秀峰游人太多，我们就不去独秀峰。今天是星期六。独秀峰游人太多，所以我们去象鼻山玩。（2）如果马会飞或羊吃草，则母鸡就会是飞鸟，如果母鸡是飞鸟，那么烤熟的鸭子还会跑。烤熟的鸭子不会跑。所以，羊不吃草。证明：（1）P：今天是星期六，Q：我们要到独秀峰去玩，R：我们要到象鼻山去玩，S：独秀峰游人太多。P→(Q←∣→R)，S→┐Q，P，S⇒R（1）SP（2）S→┐QP（3）┐QT（1），（2）I（4）PP（5）P→(Q←∣→R)P（6）Q←∣→RT（4），（5）I（7）┐QT（6）I（8）RT（7）I（2）P：马会飞，Q：羊吃草，R：母鸡就会是飞鸟，S：烤熟的鸭子会跑。（P∨Q）→R，R→S，┐S⇒┐Q（1）┐SP（2）R→SP（3）┐RT（1），（2）I（4）（P∨Q）→RP（5）┐（P∨Q）T（3），（4）I（6）┐P∧┐QT（5）E（7）┐QT（6）I习题二1.用谓词表达式符号化下列命题。（1）小王不是学生。（2）小王聪明而又好学。（3）小王和小张是好朋友。（4）他是田径或球类运动员。（5）若m是奇数，则2m不是奇数。（6）每一个有理数都是实数。（7）某些实数是有理数。（8）并非每一个实数都是有理数。（9）每一个自然数不是奇数就是偶数。（10）不管黑猫白猫，抓住老鼠就是好猫。（11）有会说话的机器人。（12）有的人不吃萝卜，但人都要喝水。解： （1）S(x)：x是学生。w：小王。┐S(w)（2）C(x)：x聪明。S(x)：x好学。w：小王。C(w)∧S(w)（3）F(x，y)：x和y是好朋友。w：小王。z：小张。F(w，z)（4）S(x)：x是田径运动员。B(x)：x是球类运动员。h：他。S(h)∨B(h)（5）O(x)：x是奇数。O(m)→┐O(2m)。（6）Q(x)：x是有理数。R(x)：x是实数。("x)(Q(x)→R(x))（7）Q(x)：x是有理数。R(x)：x是实数。($x)(R(x)∧Q(x))（8）Q(x)：x是有理数。R(x)：x是实数。┐("x)(R(x)→Q(x))（9）N(x)：x是自然数。O(x)：x是奇数。E(x)：x是偶数。("x)(N(x)→(O(x)←∣→E(x)))（10）B(x)：x是黑猫。W(x)：x是白猫。G(x)：x是好猫。Z(x)：x抓住老鼠。论域为{猫}。("x)((B(x)∨W(x))∧Z(x)→G(x))（11）M(x)：x是机器人。T(x)：x会说话。($x)(M(x)∧T(x))（12）M(x)：x是人。E(x)：x吃萝卜。D(x)：x喝水。($x)(M(x)∧┐E(x))∧("x)(M(x)→D(x))2.用谓词表达式符号化下列命题。（1）并非所有大学生都能成为科学家。（2）直线A平行于直线B，当且仅当直线A不相交于直线B。（3）某些运动员是大学生。（4）某些教练员是年老的，但是很健壮。（5）王教练既不年老，也不健壮。（6）某些大学生运动员是国家对选手。（7）所有运动员都钦佩某些教练。（8）有些大学生不钦佩教练。（9）并不是所有的汽车都比火车快。（10）男人一定比女人高，是不对的。（11）某些汽车慢于所有的火车，但至少有一火车快于每一汽车。（12）两个不相等的实数间，必存在第三个实数。解：（1）S(x)：x是大学生。K(x)：x是科学家。┐("x)(S(x)→K(x))（2）P(x,y)：x平行于y。C(x,y)：x与y相交。a：直线A。b：直线B。P(a,b)→←┐C(a,b)（3）S(x)：x是大学生。A(x)：x是运动员。($x)(A(x)∧S(x))（4）T(x)：x是教练员。O(x)：x是年老的。J(x)：x是健壮的。($x)(T(x)∧O(x)∧J(x))（5）O(x)：x是年老的。J(x)：x是健壮的。w：王教练。┐O(w)∧┐J(w)（6）S(x)：x是大学生。A(x)：x是运动员。G(x)：x是国家对选手。($x)(A(x)∧S(x)∧G(x))（7）A(x)：x是运动员。T(x)：x是教练员。P(x,y)：x钦佩y。("x)(A(x)→($y)(T(y)∧P(x,y)))（8）S(x)：x是大学生。T(x)：x是教练员。P(x,y)：x钦佩y。($x)(S(x)∧("y)(T(y)→┐P(x,y)))（9）C(x)：x是汽车。T(x)：x是火车。K(x,y)：x比y快。┐("x)(C(x)→("y)(T(y)→K(x,y)))（10）M(x)：x是男人。W(x)：x是女人。T(x,y)：x比y高。┐("x)(M(x)→("y)(W(y)→T(x,y)))（11）C(x)：x是汽车。T(x)：x是火车。K(x,y)：x比y快。($x)(C(x)∧("y)(T(y)→┐K(x,y)))∧($y)(T(y)∧("x)(C(x)→K(y,x)))（12）R(x)：x是实数。E(x,y)：x等于y。("x)("y)((R(x)∧R(y)∧┐E(x,y))→($z)(R(z)∧┐E(x,z)∧┐E(y,z)))3.试表示出“A是B的外祖父”，只允许用以下谓词：P(x)表示“x是人”，F(x，y)表示“x是y的父亲”，M(x，y)表示“x是y的母亲”。 解：P(A)∧P(B)∧P(C)∧F(A，C)∧M(C，B)4.利用谓词公式翻译下列命题。（1）如果有限个数的乘积为零，那么至少有一个因子等于零。（2）对于每一个实数x，存在一个更大的实数y。（3）存在实数x，y和z，使得x与y之和大于x与z之积。解：（1）N(x)：x是有限个数的乘积。Z(y)：y为零。P(x)：x的乘积为零。F(y)：y是乘积中的一个因子。("x)(N(x)∧P(x)→($y)(F(y)∧Z(y)))（2）R(x)：x是实数。Q(x,y)：y大于x。("x)(R(x)→($y)(R(y)∧Q(x,y)))（3）R(x)：x是实数。G(x,y)：x大于y。($x)($y)($z)(R(x)∧R(y)∧R(z)∧G(x+y,x·z))5.自然数一共有3条公理。（1）每个数都有惟一的一个数是它的后继数。（2）没有一个数使数1是它的后继数。（3）每个不等于1的数都有惟一的一个数是它的直接先行者。用两个谓词表达上述3条公理。解：N(x)：x是自然数。S(x,y)：y是x的后继数。（1）("x)(N(x)→($!y)(N(y)∧S(x,y)))（2）┐($x)(N(x)∧S(x,1))（3）("x)(N(x)∧┐S(x,2)→($!y)(N(y)∧S(y,x)))6.对下面的每个公式指出约束变元和自由变元。（1）("x)P(x)→P(y)（2）("x)(P(x)∧Q(x))∧($x)S(x)（3）($x)("y)(P(x)∧Q(y))→("x)R(x)（4）($x)($y)(P(x，y)∧Q(z))解：（1）x为约束变元，受("x)约束，y为自由变元。（2）(P(x)∧Q(x))的x为约束变元，受("x)约束，S(x)的x为约束变元，受($x)约束。（3）(P(x)∧Q(y))的x和y为约束变元，分别受($x)和("y)约束，R(x)的x为约束变元，受("x)约束。（4）(P(x，y)∧Q(z))的x和y为约束变元，分别受($x)和($y)约束，Q(z)中的z为自由变元。7.如果论域是集合{a，b，c}，试消去下面公式中的量词。（1）("x)P(x)（2）("x)P(x)∧("x)Q(x)（3）("x)(P(x)→Q(x))（4）("x)┐(P(x)∨("x)(P(x)解：（1）P(a)∧P(b)∧P(c)（2）(P(a)∧P(b)∧P(c))∧(Q(a)∧Q(b)∧Q(c))（3）(P(a)→Q(a))∧(P(b)→Q(b))∧(P(c)→Q(c))（4）(┐P(a)∧┐P(b)∧┐P(c))∨(P(a)∧P(b)∧P(c))8.试求下列各式的真值。（1）("x)(P(x)∨Q(x))，其中P(x)：x=1，Q(x)：x=2，论域是{1，2}。（2）("x)(P→Q(x))∨R(a)，其中P：2>1，Q(x)：x≤3，R(x)：x>5，a：5，论域是{-2，3，6}。 解：（1）("x)(P(x)∨Q(x))Û(P(1)∨Q(1))∧(P(2)∨Q(2))Û(T∨F)∧(F∨T)ÛT∧TÛT（2）("x)(P→Q(x))∨R(a)Û(P→Q(-2))∧(P→Q(3))∧(P→Q(6))∨R(a)Û(T→T)∧(T→T)∧(T→F)∨FÛT∧T∧F∨FÛF9.对下列谓词公式中的约束变元进行换名。（1）("x)($y)(P(x，z)→Q(y))→←S(x，y)（2）(("x)(P(x)→(R(x)∨Q(x)))∧($x)R(x))→($z)S(x，z)解：（1）("u)($v)(P(u，z)→Q(v))→←S(x，y)（2）(("u)(P(u)→(R(u)∨Q(u)))∧($v)R(v))→($z)S(x，z)10.对下列谓词公式中的自由变元进行代入。（1）(($y)A(x，y)→("x)B(x，z))∧($x)("z)C(x，y，z)（2）(("y)P(x，y)∧($z)Q(x，z))∨("x)R(x，y)解：（1）(($y)A(u，y)→("x)B(x，v))∧($x)("z)C(x，w，z)（2）(("y)P(u，y)∧($z)Q(v，z))∨("x)R(x，w)11.考虑以下赋值。论域D={1，2}指定常数a：1，b：2指定函数f：f(1)=2，f(2)=1指定谓词P：P(1，1)ÛT，P(1，2)ÛT，P(2，1)ÛF，P(2，2)ÛF求以下各式的真值。（1）P(a，f(a))∧P(b，f(b))（2）("x)($y)P(y，x)（3）("x)("y)(P(x，y)→P(f(x)，f(y)))解：（1）P(a，f(a))∧P(b，f(b))ÛP(1，f(1))∧P(2，f(2))ÛP(1，2)∧P(2，1)ÛT∧FÛF（2）("x)($y)P(y，x)Û("x)(P(1，x)∨P(2，x))Û(P(1，1)∨P(2，1))∧(P(1，2)∨P(2，2))Û(T∨F)∧(T∨F)ÛT∧TÛT（3）("x)("y)(P(x，y)→P(f(x)，f(y)))Û("x)((P(x，1)→P(f(x)，f(1)))∧(P(x，2)→P(f(x)，f(2))))Û((P(1，1)→P(f(1)，f(1)))∧(P(1，2)→P(f(1)，f(2))))∧((P(2，1)→P(f(2)，f(1)))∧(P(2，2)→P(f(2)，f(2))))Û((T→F)∧(T→F))∧((F→F)∧(F→T))Û(F∧F)∧(T∧T)ÛF∧TÛF12.将下面各式翻译成自然语言，然后在不同的个体域中确定它们的真值。（1）("x)($y)(x·y=0)（2）($x)("y)(x·y=0)（3）("x)($y)(x·y=1)（4）($x)("y)(x·y=1)（5）("x)($y)(x·y=x)（6）($x)("y)(x·y=x)（7）("x)("y)($z)(x-y=z)个体域分为（a）实数集合R（b）整数集合Z （c）正整数集合Z+（d）非零实数集合R-{0}解：（1）对于任意的x，存在y，使得x·y=0。（2）存在x，对于任意的y，都有x·y=0。（3）对于任意的x，存在y，使得x·y=1。（4）存在x，对于任意的y，都有x·y=1。（5）对于任意的x，存在y，使得x·y=x。（6）存在x，对于任意的y，都有x·y=x。（7）对于任意的x，任意的y，存在z，使得x-y=z。个体域分为（a）实数集合R（1）真（2）真（3）假（4）假（5）真（6）真（7）真（b）整数集合Z（1）真（2）真（3）假（4）假（5）真（6）真（7）真（c）正整数集合Z+（1）假（2）假（3）假（4）假（5）真（6）假（7）假（d）非零实数集合R-{0}（1）假（2）假（3）真（4）假（5）真（6）假（7）假13.判断下面公式的真假，如果是真，请证明之；如果为假，请给出P和Q的解释，以说明公式为假（1）("x)(P(x)→Q(x))Þ("x)P(x)→("x)Q(x)（2）("x)P(x)→("x)Q(x)Þ("x)(P(x)→Q(x))解：（1）("x)(P(x)→Q(x))Û("x)(┐P(x)∨Q(x))Û("x)┐(P(x)∧┐Q(x))Û┐($x)(P(x)∧┐Q(x))Þ┐(($x)P(x)∧($x)┐Q(x))Û┐($x)P(x)∨┐($x)┐Q(x))Û("x)┐P(x)∨("x)Q(x))Þ($x)┐P(x)∨("x)Q(x))Û┐("x)P(x)∨("x)Q(x))Û("x)P(x)→("x)Q(x)（2）("x)P(x)→("x)Q(x)Þ("x)(P(x)→Q(x))不成立。P(x)：x成绩优秀。Q(x)：x获得奖学金。论域为所有学生。("x)P(x)→("x)Q(x)表示：若所有学生成绩都优秀，则所有学生都获得奖学金。("x)(P(x)→Q(x))表示：任何一个学生，只要成绩优秀，他就获得奖学金。显然“任何一个学生，只要成绩优秀，他就获得奖学金。”可以推出“若所有学生成绩都优秀，则所有学生都获得奖学金。”反之未必成立。14.求证：($x)(P(x)→Q(x))Û("x)P(x)→($x)Q(x)证明：($x)(P(x)→Q(x))Û($x)(┐P(x)∨Q(x))Û($x)┐P(x)∨($x)Q(x))Û┐("x)P(x)∨($x)Q(x))Û("x)P(x)→($x)Q(x)15.求证：("x)("y)(P(x)→Q(y))Û($x)P(x)→("y)Q(y)证明：("x)("y)(P(x)→Q(y))Û("x)("y)(┐P(x)∨Q(y))Û("x)┐P(x)∨("y)Q(y)Û┐($x)P(x)∨("y)Q(y)Û($x)P(x)→("y)Q(y)16.下列推导过程中有何错误？（1）("x)(P(x)→Q(x))P（2）P(a)→Q(a)US(1)（3）($x)P(x)P（4）P(a)ES(3)（5）Q(a)T(2),(4)I（6）($x)Q(x)EG(5) 解：应先消去存在量词。17.把以下各式化为前束范式。（1）("x)(P(x)→($y)Q(x，y))（2）($x)(┐(($y)P(x，y))→(($z)Q(z)→R(x)))（3）("x)("y)((($z)P(x，y，z)∧($u)Q(x，u))→($v)Q(y，v))解：（1）("x)(P(x)→($y)Q(x，y))Û("x)(┐P(x)∨($y)Q(x，y))Û("x)($y)(┐P(x)∨Q(x，y))（2）($x)(┐(($y)P(x，y))→(($z)Q(z)→R(x)))Û($x)(($y)P(x，y)∨(($z)Q(z)→R(x)))Û($x)(($y)P(x，y)∨(┐($z)Q(z)∨R(x)))Û($x)(($y)P(x，y)∨(("z)┐Q(z)∨R(x)))Û($x)($y)("z)(P(x，y)∨┐Q(z)∨R(x))（3）("x)("y)((($z)P(x，y，z)∧($u)Q(x，u))→($v)Q(y，v))Û("x)("y)(┐(($z)P(x，y，z)∧($u)Q(x，u))∨($v)Q(y，v))Û("x)("y)(("z)┐P(x，y，z)∨("u)┐Q(x，u))∨($v)Q(y，v))Û("x)("y)("z)("u)($v)(┐P(x，y，z)∨┐Q(x，u)∨Q(y，v))18.求等价于下面各式的前束析取范式和前束合取范式。（1）(($x)P(x)∨($x)Q(x))→($x)(P(x)∨Q(x))（2）("x)(P(x)→("y)(("z)Q(x，y)→┐("z)R(y，x)))（3）("x)P(x)→($x)(("z)Q(x，z)∨("z)R(x，y，z))（4）("x)(P(x)→Q(x，y))→(($y)P(y)∧($z)Q(y，z))解：（1）(($x)P(x)∨($x)Q(x))→($x)(P(x)∨Q(x))因为(($x)P(x)∨($x)Q(x))Û($x)(P(x)∨Q(x))，所以(($x)P(x)∨($x)Q(x))→($x)(P(x)∨Q(x))为永真式，不写为前束范式的形式。（2）("x)(P(x)→("y)(("z)Q(x，y)→┐("z)R(y，x)))Û("x)(┐P(x)∨("y)(Q(x，y)→┐R(y，x)))Û("x)("y)(┐P(x)∨┐Q(x，y)∨┐R(y，x)))前束合取范式Û("x)("y)((┐P(x)∧Q(x，y)∧R(y，x))∨(┐P(x)∧Q(x，y)∧┐R(y，x))∨(┐P(x)∧┐Q(x，y)∧R(y，x))∨(┐P(x)∧┐Q(x，y)∧┐R(y，x))∨(P(x)∧┐Q(x，y)∧R(y，x))∨(P(x)∧┐Q(x，y)∧┐R(y，x))∨(P(x)∧Q(x，y)∧┐R(y，x)))前束析取范式（3）("x)P(x)→($x)(("z)Q(x，z)∨("z)R(x，y，z))Û┐("x)P(x)∨($x)(("z)Q(x，z)∨("z)R(x，y，z))Û($x)┐P(x)∨($x)(("z)Q(x，z)∨("u)R(x，y，u))Û($x)(┐P(x)∨("z)Q(x，z)∨("u)R(x，y，u))Û($x)("z)("u)(┐P(x)∨Q(x，z)∨R(x，y，u))前束合取范式Û($x)("z)("u)((┐P(x)∧Q(x，z)∧R(x，y，u))∨(┐P(x)∧Q(x，z)∧┐R(x，y，u))∨(┐P(x)∧┐Q(x，z)∧R(x，y，u))∨(┐P(x)∧┐Q(x，z)∧┐R(x，y，u))∨(P(x)∧Q(x，z)∧R(x，y，u))∨(P(x)∧Q(x，z)∧┐R(x，y，u))∨(P(x)∧┐Q(x，z)∧R(x，y，u)))前束析取范式（4）("x)(P(x)→Q(x，y))→(($y)P(y)∧($z)Q(y，z))Û┐("x)(┐P(x)∨Q(x，y))∨(($y)P(y)∧($z)Q(y，z))Û($x)(P(x)∧┐Q(x，y))∨(($u)P(u)∧($z)Q(y，z))Û($x)($u)($z)((P(x)∧┐Q(x，y))∨(P(u)∧Q(y，z))前束析取范式Û($x)($u)($z)((P(x)∨P(u))∧(P(x)∨Q(y，z))∧(┐Q(x，y)∨P(u))∧(┐Q(x，y)∨Q(y，z)))前束合取范式19.求下列各式的斯柯伦范式。 （1）("x)P(x)∧┐($x)Q(x)（2）($x)P(x)→("x)Q(x)（3）(("x)P(x)∨($y)Q(y))→("x)R(x)（4）("x)(P(x)→Q(x，y))→(($y)R(y)→($z)S(y，z))解：（1）("x)P(x)∧┐($x)Q(x)Û("x)P(x)∧┐($y)Q(y)Û($y)("x)(P(x)∧┐Q(y))（2）($x)P(x)→("x)Q(x)Û($x)P(x)→("y)Q(y)Û($x)("y)(P(x)→Q(y))（3）(("x)P(x)∨($y)Q(y))→("x)R(x)Û┐(("x)P(x)∨($y)Q(y))∨("x)R(x)Û(┐("x)P(x)∧┐($y)Q(y))∨("x)R(x)Û(($x)┐P(x)∧("y)┐Q(y))∨("x)R(x)Û($x)("y)("z)(┐P(x)∧┐Q(y)∨R(z))（4）("x)(P(x)→Q(x，y))→(($y)R(y)→($z)S(y，z))Û┐("x)(P(x)→Q(x，y))∨(($y)R(y)→($z)S(y，z))Û($x)(P(x)∧┐Q(x，y))∨(("y)┐R(y)∨($z)S(y，z))Û($x)($z)("y)(P(x)∧┐Q(x，u)∨┐R(y)∨S(v，z))20.证明下列各式。（1）("x)(┐A(x)→B(x))，("x)┐B(x)Þ($x)A(x)（2）($x)A(x)→("x)B(x)Þ("x)(A(x)→B(x))（3）("x)(A(x)→B(x))，("x)(C(x)→┐B(x))Þ("x)(C(x)→┐A(x))（4）("x)(A(x)∨B(x))，("x)(B(x)→┐C(x))，("x)C(x)Þ("x)A(x)证明：（1）(1)("x)┐B(x)P(2)┐B(a)ES(1)(3)("x)(┐A(x)→B(x))P(4)┐A(a)→B(a)US(3)(5)A(a)T(2)(4)I(6)($x)A(x)EG(5)（2）($x)A(x)→("x)B(x)Û┐($x)A(x)∨("x)B(x)Û("x)┐A(x)∨("x)B(x)Þ("x)(┐A(x)∨B(x))Û("x)(A(x)→B(x))（3）(1)("x)(C(x)→┐B(x))P(2)C(a)→┐B(a)US(1)(3)("x)(A(x)→B(x))P(4)A(a)→B(a)US(3)(5)┐B(a)→┐A(a)T(4)E(6)C(a)→┐A(a)T(2)(5)I(7)("x)(C(x)→┐A(x))UG(6)（4）("x)(A(x)∨B(x))，("x)(B(x)→┐C(x))，("x)C(x)Þ("x)A(x)(1)("x)C(x)P(2)C(a)US(1)(3)("x)(B(x)→┐C(x))P (4)B(a)→┐C(a)US(3)(5)┐B(a)T(2)(4)I(6)("x)(A(x)∨B(x))P(7)A(a)∨B(a)US(6)(8)A(a)T(5)(7)I(9)("x)A(x)UG(8)21.用CP规则证明。（1）("x)(P(x)→Q(x))Þ("x)P(x)→("x)Q(x)（2）("x)(P(x)∨Q(x))Þ("x)P(x)∨($x)Q(x)证明：（1）("x)(P(x)→Q(x))Þ("x)P(x)→("x)Q(x)证明：(1)("x)P(x)P(附加前提)(2)P(a)ES(1)(3)("x)(P(x)→Q(x))P(4)P(a)→Q(a)US(3)(5)Q(a)T(2)(4)I(6)("x)Q(x)UG(5)(7)("x)P(x)→("x)Q(x)CP(1)(6)（2）("x)(P(x)∨Q(x))Þ("x)P(x)∨($x)Q(x)证明：(1)┐("x)P(x)P(附加前提)(2)($x)┐P(x)T(1)E(3)┐P(a)ES(2)(4)("x)(P(x)∨Q(x))P(5)P(a)∨Q(a)US(4)(6)Q(a)T(3)(5)I(7)($x)Q(x)EG(6)(8)┐("x)P(x)→($x)Q(x)CP(1)(7)(9)("x)P(x)∨($x)Q(x)T(8)E22.符号化下列命题，并推证其结论：（1）任何人如果他喜欢步行，他就不喜欢乘汽车。每一个人或者喜欢汽车或者喜欢骑自行车。有的人不爱骑自行车。因而有人的不爱步行。（2）不存在能表示成分数的无理数。有理数都能表示成分数。因此，有理数都不是无理数。（3）每个自然数不是奇数就是偶数。自然数是偶数当且仅当它能被2整除。并不是所以的自然数都能被2整除。因此，有的自然数是奇数。（4）三角函数都是周期函数。一些三角函数是连续函数。所以，一些周期函数是连续函数。（5）每个科学家都是勤奋的。每个勤奋又身体健康的人在事业中都会获得成功。存在着身体健康的科学家。所以存在着事业获得成功的人或事业半途而废的人。解：（1）F(x)：x喜欢步行。C(x)：x喜欢喜欢乘汽车。B(x)：x喜欢骑自行车。论域是{人}。("x)(F(x)→┐C(x))，("x)(C(x)∨B(x))，($x)┐B(x)Þ($x)┐F(x)证明：(1)($x)┐B(x)P (2)┐B(a)ES(1)(3)("x)(C(x)∨B(x))P(4)C(a)∨B(a)US(3)(5)C(a)T(2)(4)I(6)("x)(F(x)→┐C(x))P(7)F(a)→┐C(a)US(6)(8)C(a)→┐F(a)T(7)E(9)┐F(a)T(5)(8)I(10)($x)┐F(x)EG(9)（2）Q(x)：x是有理数。W(x)：x是无理数。D(x)：x能表示成分数。┐($x)(W(x)∧D(x))，("x)(Q(x)→D(x))Þ("x)(Q(x)→┐W(x))证明：(1)┐($x)(W(x)∧D(x))P(2)("x)┐(W(x)∧D(x))T(1)E(3)("x)(W(x)→┐D(x))T(2E(4)W(a)→┐D(a)US(3)(5)D(a)→┐W(a)T(4)E(6)("x)(Q(x)→D(x))P(7)Q(a)→D(a)US(6)(8)Q(a)→┐W(a)T(5)(7)I(9)("x)(Q(x)→┐W(x))UG(8)（3）O(x)：x是奇数。E(x)：x是偶数。D(x)：x能被2整除。论域为{自然数}。("x)(O(x)←∣→E(x))，("x)(E(x)→←D(x))，┐("x)D(x)Þ($x)O(x)证明：(1)┐("x)D(x)P(2)($x)┐D(x)T(1)E(3)┐D(a)ES(2)(4)("x)(E(x)→←D(x))P(5)E(a)→←D(a)US(4)(6)┐E(a)T(3)(5)I(7)("x)(O(x)←∣→E(x))P(8)O(a)←∣→E(a)US(7)(9)O(a)T(6)(8)I(10)($x)O(x)EG(9)（4）S(x)：x是三角函数。D(x)：x是周期函数。H(x)：x是连续函数。论域是{函数}。("x)(S(x)→D(x))，($x)(S(x)∧H(x))Þ($x)(D(x)∧H(x))证明：(1)($x)(S(x)∧H(x))P(2)S(a)∧H(a)ES(1)(3)S(a)T(2)I(4)H(a)T(2)I(5)("x)(S(x)→D(x))P(6)S(a)→D(a)US(5)(7)D(a)T(3)(6)I (8)D(a)∧H(a)T(4)(7)I(9)($x)(D(x)∧H(x))EG(8)（5）S(x)：x是科学家。D(x)：x是勤奋的。H(x)：x是身体健康的。C(x)：x是成功的。论域是{人}。("x)(S(x)→D(x))，("x)(D(x)∧H(x)→C(x))，($x)(S(x)∧H(x))Þ($x)C(x)∨($x)┐C(x)证明：(1)($x)(S(x)∧H(x))P(2)S(a)∧H(a)ES(1)(3)S(a)T(2)I(4)H(a)T(2)I(5)("x)(S(x)→D(x))P(6)S(a)→D(a)US(5)(7)D(a)T(3)(6)I(8)("x)(D(x)∧H(x)→C(x))P(9)D(a)∧H(a)→C(a)US(8)(10)C(a)T(4)(7)(9)I(11)($x)C(x)EG(10)(12)($x)C(x)∨($x)┐C(x)T(11)I习题三1.分别用描述法和列举法表示下列集合：(1)非负偶数集；(2)整数24的全部正因子的集合；(3)不超过9且与9互质的正整数集合（该集合的元素个数称欧拉函数j(9)）。解：描述法（1）{x|x是非负偶数}（2）{x|x是24的正因子}（3）{x|x是不超过9且与9互质的正整数}列举法（1）{0,2,4,…}（2）{1,2,3,4,6,8,12,24}（3）{1,2,4,5,7,8}2.是否存在集合A和B，使得A⊆B且AÎB？若存在，请举一例。解：存在。A={1}，B={1,{1}}，则A⊆B且AÎB均成立。3.求下列集合的幂集：（1）Æ；（2）{Æ}；（3）{a,{a}}；（4）{{1,2}}。解：（1）P(Æ)={Æ}（2）P({Æ})={Æ,{Æ}} （3）P({a,{a}})={Æ,{a},{{a}},{a,{a}}}（4）P({{1,2}})={Æ,{{1,2}}}4.设S={0,1}，求集合S×P(S)。解：P(S)={Æ,{0},{1},{0,1}}S×P(S)={<0,Æ>,<0,{0}>,<0,{1}>,<0,{0,1}>,<1,Æ>,<1,{0}>,<1,{1}>,<1,{0,1}>}5.证明：对任意集合A，B都有P(A)∩P(B)＝P(A∩B)，P(A)∪P(B)⊆P(A∪B)并举例说明，一般P(A)∪P(B)≠P(A∪B)。证明：对任意的集合C，若C∈P(A)∩P(B)ÛC∈P(A)∧C∈P(B)ÛC⊆A∧C⊆BÛC⊆A∩B所以P(A)∩P(B)＝P(A∩B)成立。对任意的集合C，若C∈P(A)∪P(B)ÛC∈P(A)∨C∈P(B)ÛC⊆A∨C⊆BÞC⊆A∪B所以P(A)∪P(B)⊆P(A∪B)成立。举例：A={1,2}，B={2,3}，P(A)={Æ，{1}，{2}，{1,2}}，P(B)={Æ，{2}，{3}，{2,3}}，P(A)∪P(B)={Æ，{1}，{2}，{1,2}，{3}，{2,3}}，A∪B={1,2,3}，P(A∪B)={Æ，{1}，{2}，{1,2}，{3}，{2,3}，{1,3}，{1,2,3}}。所以，P(A)∪P(B)≠P(A∪B)。6.设A，B，C是任意集合，证明：（1）C∩(AÅB)=(C∩A)Å(C∩B)；（2）已知A∩B⊆B∩C，且有A-B⊆B-C，则A⊆B。证明：（1）C∩(AÅB)=C∩((A－B)∪(B－A))=(C∩(A－B))∪(C∩(B－A))=((C∩A)－(C∩B))∪((C∩B)－(C∩A))=(C∩A)Å(C∩B)（2）反证法。假设结论不成立，则存在x∈A，且xÏB，则x∈A-B，x∈B-C，即x∈B。与xÏB矛盾。7.确定下列关系具备哪些性质？（1）当且仅当|i-k|<11(i,kÎZ)时，有iRk；（2）当且仅当mn>8(m,nÎN)时，有mRn；（3）当且仅当i≤k(i,kÎN)时，有iRk。解：（1）自反，对称（2）对称（3）自反，对称，传递8.请在集合A＝{a,b,c}上分别构造满足下述要求的二元关系：（1）既是对称又是反对称的；（2）既不自反也不反自反；（3）对称且自反；（4）自反,对称且传递；（5）以{,}为子集而且还是传递的。 解：（1）{,,}（2）{,}（3）{,,,,}（4）{,,,,}（5）{,}9.设Rj表示Z上模j等价关系，Rk表示Z上模k等价关系,证明：Z/Rk细分Z/Rj当且仅当k是j的整数倍。证明：充分性：若k是j的整数倍，即$lÎZ，使k=lj，Z/Rk={[a]Rk|aÎZ}，Z/Rj={[a]Rj|aÎZ}，[a]Rk={x|xÎZ∧aRkx}，[a]Rj={x|xÎZ∧aRjx}，显然对任意的xÎ[a]Rk，aºx(modk)，即$mÎZ，使得a-x=km=ljm=lmj，即xÎ[a]Rj，因此Z/Rk细分Z/Rj。必要性：若Z/Rk细分Z/Rj，即[a]Rk⊆[a]Rj，显然Î[a]Rk，因此Î[a]Rj，所以k-0=1·k=c·j，cÎZ，于是k是j的整数倍。10.证明：若关系R是对称的,则Rk(k≥1,kÎN)也是对称的。证明：设R是A上的二元关系，"x，yÎA，若xRky成立，则由关系复合的定义，存在x0=x,x1,x2,…xk-1,xk=y，使得x0Rx1,x1Rx2,…,xk-1Rxk成立，由R是对称的,故xkRxk-1,xk-1Rxk-2,…,x2Rx1,x1Rx0成立,再由关系复合的定义，有xkRkx0成立，即yRkx，因而Rk(k≥1,kÎN)是对称的。11.设集合A={a,b,c,d}上的关系R={,,,}，用矩阵运算求出R的自反、对称和传递闭包。解：，，,∨=。所以r(R)={,,,,,,}∨=所以s(R)={,,,,} 所以t(R)={,,,,,,,,}12.设R和S是A上的二元关系，且R⊆S，证明：（1）r(R)⊆r(S)（2）s(R)⊆s(S)（3）t(R)⊆t(S)证明：（1）"Îr(R),由r(R)的定义有ÎRÚÎIA,若ÎR,由R⊆S,Îr(S),若ÎIA,有Îr(S),所以r(R)⊆r(S)。（2）"Îs(R)，由s(R)的定义有ÎRÚÎR-1,若ÎR,由R⊆S,Îs(S),若ÎR-1,有ÎR,因而ÎS,所以ÎS-1,即Îs(S)，所以s(R)⊆s(S)。（3）"Ît(R),由t(R)的定义有ÎRk(k≥1,kÎN)，即存在x0=x,x1,x2,…xk-1,xk=y，使得x0Rx1,x1Rx2,…,xk-1Rxk成立，由R⊆S,因而x0Sx1,x1Sx2,…,xk-1Sxk成立，所以ÎSk(k≥1,kÎN)，即Ît(S),因而t(R)⊆t(S)。13.设R和S是A上的二元关系，证明：（1）r(R∪S)=r(R)∪r(S)（2）s(R∪S)=s(R)∪s(S)（3）t(R)∪t(S)⊆t(R∪S)证明：（1）r(R∪S)=(R∪S)∪IA=(R∪IA)∪(S∪IA)=r(R)∪r(S)。（2）s(R∪S)=(R∪S)∪(R∪S)-1=(R∪S)∪(R-1∪S-1)=(R∪R-1)∪(S∪S-1)=s(R)∪s(S)。（3）t(R)∪t(S)=∪，t(R∪S)==∪∪，显然t(R)∪t(S)⊆t(R∪S)。 14.求集合{a，b，c，d}的所有划分和等价关系。解：集合{a，b，c，d}中共有4个元素，可作如下划分：1)4＝1＋1＋1＋1型划分，只有一个，即{{a}，{b}，{c}，{d}}，对应的等价关系为：{，，，}。2)4＝2＋1＋1型划分，有＝6个，即{{a，b}，{c}，{d}}，{{a，c}，{b}，{d}}，{{a，d}，{b}，{c}}，{{b，c}，{a}，{d}}，{{b，d}，{a}，{c}}，{{c，d}，{a}，{b}}，对应的等价关系为：{，，，，，}，{，，，，，}，{，，，，，}，{，，，，，}，{，，，，，}，{，，，，，}。3)4＝3＋1型划分，有＝4个，即{{a，b，c}，{d}}，{{a，b，d}，{c}}，{{a，c，d}，{b}}，{{b，c，d}，{a}}，对应的等价关系为：{，，，，，，，，，}，{，，，，，，，，，}，{，，，，，，，，，}，{，，，，，，，，，}。4)4＝2＋2型划分，有＝3个，即{{a，b}，{c，d}}，{{a，c}，{b，d}}，{{a，d}，{b，c}}，对应的等价关系为：{，，，，，，，}，{，，，，，，，}，{，，，，，，，}。5)4＝4＋0型划分，有1个，即{{a，b，c，d}}，对应的等价关系为：{，，，，，，，，，，，，，，，}。综上，集合{a，b，c，d}的划分和等价关系共有15个。15.设R是非空集合A上的二元关系。如果对"a,b,c∈A满足aRb且bRcÞcRa，则称R为A上循环关系。证明：R是自反和循环的关系当且仅当R是等价关系。证明：必要性：若R是自反和循环的，对"a,b,c∈A，aRa成立，若aRc成立，由R是循环的，有cRa，因此R是对称的，再若aRb且bRc，由R是循环的，有cRa，再由R是对称的，有aRc，因此R是传递的，因而R是等价关系。充分性：若R是等价关系，则显然R是自反的，只需证R是循环的。对"a,b,c∈A，若aRb且bRc，由R的传递性，有aRc，再由R的对称性，有cRa，因此R是循环的。16.设A,B是非空集合，f是从A到B的映射。定义A上二元关系R为：x，y∈A,xRy当且仅当f(x)=f(y)证明：R是A上等价关系，并描述由R生成的A的划分。证明：显然f(x)=f(x)，因此xRx当，即R是自反的。若xRy，有f(x)=f(y)，因此f(y)=f(x)，所以yRx，即R是对称的。若xRy，yRz，有f(x)=f(y)，f(y)=f(z)，因此f(x)=f(z)，所以xRz，即R是传递的。 因此R是A上等价关系。由R生成的A的划分中凡是对应的值相同的自变量属于同一分块。17.给出一个既是等价关系又是偏序关系的二元关系。解：A＝{a,b,c}上的R={,,}。18.设A1、A2和A3是全集U的子集，则形如Ai¢(Ai¢为Ai或~Ai)的集合称为由A1、A2和A3产生的小项。试证由A1、A2和A3所产生的所有非空小项的集合构成全集U的一个划分。证明：（1）Ai¢¹Æ（2）Ai¢∩Aj¢=Æ（3）(A1∩A2∩A3)∪(A1∩A2∩~A3)∪(A1∩~A2∩A3)∪(A1∩~A2∩~A3)∪(~A1∩A2∩A3)∪(~A1∩A2∩~A3)∪(~A1∩~A2∩A3)∪(~A1∩~A2∩~A3)=(A1∩A2)∪(A1∩~A2)∪(~A1∩A2)∪(~A1∩~A2)=A1∪~A1=U因此，由A1、A2和A3所产生的所有非空小项的集合构成全集U的一个划分。19.设R和S是A上的相容关系，问：（1）复合关系RS是A上的相容关系吗？（2）R∩S是A上的相容关系吗？（3）R∪S是A上的相容关系吗？解：（1）设A={1,2,3}，R={<1,1>,<2,2>,<3,3>,<1,2>,<2,1>}，S={<1,1>,<2,2>,<3,3>,<2,3>,<3,2>}，RS={<1,1>,<2,2>,<3,3>,<1,2>,<2,1>,<2,3>,<3,2>,<1,3>}，不是相容关系。（2）R∩S显然是自反的，∈R∩S，则∈R且∈S，因而∈R且∈S，即∈R∩S，因此R∩S是A上的相容关系。（3）R∪S显然是自反的，∈R∪S，则∈R或∈S，因而∈R或∈S，即∈R∪S，因此R∪S是A上的相容关系。是A上的相容关系。20.画出集合S={1,2,3,4,5,6}在偏序关系“整除”下的哈斯图，（1）写出{1,2,3,4,5,6}的最大(小)元和极大(小)元；（2）分别写出{2,3,6}和{2,3,5}的上(下)界、上(下)确界。解：哈斯图如下：{1,2,3,4,5,6}的最大元：无。{1,2,3,4,5,6}的最小元：1。{1,2,3,4,5,6}的极大元：4、5、6。{1,2,3,4,5,6}的极小元：1{2,3,6}的上界：6。{2,3,6}的下界：1。{2,3,6}的上确界：6。{2,3,6}的下确界：1。{2,3,5}的上界：无。{2,3,5}的下界：1。{2,3,5}的上确界：无。{2,3,5}的下确界：1。习题四1.分析下列各个函数，指出其性质（入射、满射或双射）（1）f:Z→Z,f(j)=jmod3 （2）f:N→N，（3）f:N→{0,1}，（4）f:Z→N，f(i)=|2i|+1（5）f:R→R，f(r)=2r–15解：（1）、（2）、（4）既不是入射，也不是满射。（3）是满射。（5）是双射。2.假设f和g是函数，求证f∩g也是函数。证明：f∩g={|xÎdomf∧xÎdomg∧y=f(x)∧y=g(x)}={|xÎdomf∩domg∧y=f(x)=g(x)}令h=f∩g，则domh={x|xÎdomf∩domg∧f(x)=g(x)}若y1¹y2，因为f是函数，故必有y1=f(x1)，y2=f(x2)，且x1¹x2，所以h=f∩g是一个函数。因为domh存在且y1¹y2时x1¹x2，即h={|xÎdomh，y=h(x)=f(x)=g(x)}3.设A={1，2，…，n}，证明从A到A的任意单射函数必是满射函数，其逆亦真。证明：设f是从A到A的单射函数，则|A|=|f(A)|，因为f是A到A的函数，所以f(A)ÍA，又因为|A|=|f(A)|，且|A|是有限的，因此必有f(A)=A，即f是满射函数。反之，若f是从A到A的满射函数，根据满射定义有，f(A)=A，于是|A|=|f(A)|，又由|A|是有限的，故f是从A到A的单射函数。4.证明从N×N到N的函数f(x，y)=x+y和g(x，y)=x∙y是满射，但不是单射。证明：对任意zÎN，显然存在0，1，zÎN，使得0+z=z，1∙z=z，因而f(x，y)=x+y和g(x，y)=x∙y是满射。由于3+2=4+1=5，因而f(x，y)=x+y不是单射，由于3∙2=6∙1=6，因而g(x，y)=x∙y不是单射。5.试给出满足下列条件的函数例子。（1）是单射而不是满射。（2）是满射而不是单射。（3）不是单射也不是满射。（4）既是单射又是满射。解：（1）设A={a,b,c}，B={1,2,3,4}，f={,,}。（2）设A={a,b,c}，B={1,2}，f={,,}。（3）设A={a,b,c}，B={1,2,3,4}，f={,,}。（4）设A={a,b,c}，B={1,2,3}，f={,,}。6.有限集A和B，|A|=m，|B|=n，问：（1）A到B的不同的二元关系有多少？（2）从A到B存在多少不同的函数？（3）从A到B存在入射的条件是什么？有多少不同的入射？（4）从A到B存在满射的条件是什么？有多少不同的满射？（5）从A到B存在双射的条件是什么？有多少不同的双射？ 解：（1）2mn。（2）nm。（3）m≤n，。（4）n≤m，n!S(m，n)。(本题具有一定的难度，S(m，n)的意义请参见9.5节，本题即第9章44题。)（5）m=n，m！。7.证明：（1）f(A∪B)=f(A)∪f(B)（2）f(A∩B)Íf(A)∩f(B)（3）f(A)-f(B)Íf(A-B)证明：（1）对任意的yÎf(A∪B)有，yÎf(A∪B)Û$xÎA∪B∧f(x)=yÛ$xÎA∨$xÎB∧f(x)=yÛ($xÎA∧f(x)=y)∨($xÎB∧f(x)=y)ÛyÎf(A)∨yÎf(B)ÛyÎf(A)∪f(B)（2）对任意的yÎf(A∩B)有，yÎf(A∩B)Û$xÎA∩B∧f(x)=yÛ$xÎA∧$xÎB∧f(x)=yÞ($x1ÎA∧f(x1)=y)∧($x2ÎB∧f(x2)=y)ÛyÎf(A)∧yÎf(B)ÛyÎf(A)∩f(B)（3）对任意的yÎf(A)-f(B)有，yÎf(A)∧yÏf(B)。即对某个x1ÎA，y=f(x1)，但对任意xÎB，yÏf(x)。故对某个x1ÎA-B，y=f(x1)，即yÎf(A-B)于是f(A)-f(B)Íf(A-B)。8.设f:A→B是满射函数，且函数g:B→P(A)定义为:g(b)={x|x∈A∧f(x)=b}证明：g是单射。其逆成立吗？若成立给出证明，否则给出例子予以说明。证明：因为f是满射函数，则对任意b∈B，至少存在一个x∈A，使得f(x)=b，故g的定义域为B。对任意的b1，b2ÎB，且b1¹b2，g(b1)={x|x∈A∧f(x)=b1}g(b2)={y|y∈A∧f(y)=b2}因为b1¹b2，f(x)¹f(y)，而f是函数，故x¹y，所以g(b1)¹g(b2)故g是单射。逆不成立。例如：A={a,b,c}，B={x,y,z}，则f:A→B，f(a)=x，f(b)=x，f(c)=y。g:B→P(A)，g(x)={a,b}，g(y)={c}，g(z)=Æ。g是单射，但f不是满射。9.证明：若f:A→B，g:B→A，且gf=IA，fg=IB，则g=f-1，且f=g-1。证明：因为gf=IA，所以gf(a1)=g(f(a1))=a1，gf(a2)=g(f(a2))=a2，若a1≠a2，g(f(a1))≠g(f(a2))，所以f(a1)≠f(a2)，即f:是入射。又对任意的aÎA有gf(a)=g(f(a))=a，即存在f(a)=bÎB，使得g(b)=a，因此g是满射。同理，若fg=IB，则g是入射且f是满射，故可知f和g都是双射函数。设Îf，因为ÎIA，而gf=IA，故必有某个cÎB，使得Îf且Îg，由Îf∧Îf⇒b=c因此Îg。反之，若Îg，由ÎIB，故必有某个dÎA，有Îg∧Îf，由Îg∧Îg⇒a=d因此Îf。上述证明得到Îf当且仅当Îg，所以g=f-1且f=g-1。10.证明：若(gf)-1是一个函数，则f和g不一定是入射。 证明：设A={a,b,c}，B={1,2,3,4}，C={x,y,z}，f是A到B的函数，g是B到C的函数，f={,,}，g={<1,x>,<2,x>,<3,y>,<4,z>},则gf={,,}，(gf)-1={,,}是双射函数，但g不是入射。'